以前（2013年9月13日の投稿）、ガンマ線のパルスをオシロで観測した時の分布について書きましたが、より詳しく調べました。
ガンマ線のパルスを一定時間カウントすると、その数はばらついて一定の値ではありません。カウント数が非常に多いとばらつきはガウス分布になりますが、カウント数が少ない時はポアソン分布になります。また、パルスの時間間隔は指数分布になります。今回、この指数分布になっている事を確認しました。

観測方法は次のとおりです。
１．フォトマルからの電流を50Ωの抵抗で電圧に変換し、10倍のアンプで増幅した後、0.2Vの閾値でディスクリし、500nsecの幅、電圧１Vのパルスに変換します。
２．そのパルスをカウンタ（53230A）に入力し、パルス間隔を測定し、ヒストグラムを作成します。5msecの間をビン幅50μsecで100個のビンに振り分けカウントします。

次のグラフは２インチシンチレータ、Cs137、約１μSv/h程度の線量率のもとで、100000個のパルスについて測定した結果です。

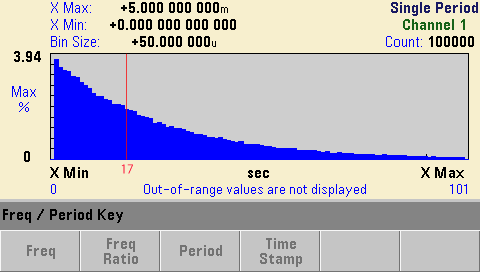
縦軸は％表示で、グラフは、ほぼ理論どおりの、指数関数のカーブになっています。指数分布（λ Exp(-λx))のλは0.04で、時間間隔の平均値は1/λ=25（1.25msec間隔）となります。0から平均値までの累積確率は0.63ですので、多くのパルスは平均より短い間隔で発生しています。累積確率が半分になるのはx=17（0.85msec)程度の時で、1秒間に平均1176個のパルスが発生している事になります。

グラフからも分かるように、一つのパルスが発生した後、すぐに次のパルスが発生する確率が高いので、ガンマ線の検出システムではデッドタイムを短くする事が重要です。デッドタイムがどの程度の誤差になるかですが、今回の測定結果からは、50μsecあると１μSv/hでは約4％の数え落としが発生すると推定できます。この誤差は線量率が高くなるに従い大きくなるので線量率毎の補正が必要となります。